In this post, I’m excited to dive into the research I conducted with a colleague and friend, titled “Scalable Multi-User Precoding and Pilot Optimization with Graph Neural Networks,” which was published at IEEE ICC 2024 (Rizzello et al., 2024). We’ll explore the problem that inspired our work, the key solution we proposed, and the results we discovered.
What is this research about?
At a high level, this research looks at how a base station (the big tower in your neighborhood) can serve many users at the same time without causing interference. The goal is to design the system so that when the tower sends a message to your phone, it arrives clearly, without getting mixed up with signals intended for other users in the same cell.
To avoid interference, the base station needs to understand the surrounding environment. This is where Channel State Information (CSI) comes in. Think of CSI as a detailed, real-time map showing exactly how a wireless signal travels between your phone and the tower. It accounts for every obstacle—buildings, cars, trees, and even people—and shows how signals bounce off them.
In a frequency division duplex system1, the base station cannot directly measure CSI. Instead, it relies on feedback from your phone in a three-step process:
- The tower sends pilot signals to your phone.
- Your phone receives them and estimates the CSI.
- Your phone sends that CSI back to the tower.
With this map in hand, the base station can perform precoding. Precoding is like adjusting the shape and direction of the signal before it leaves the tower so that it arrives at your phone exactly as intended. Imagine it as a smart spotlight: the base station tweaks the beam’s angle and focus to hit your phone perfectly while avoiding other users nearby. Without precoding, the signals would scatter, causing interference and reducing network performance.
Traditionally, precoding is handled as a separate step, relying on a clean channel estimate beforehand. In our work, we take a different route. Instead of breaking the problem into separate steps, we take an end-to-end approach. In our system, we don’t perform channel estimation explicitly. Rather, we design several blocks together at once: the pilot signals, a feature extractor (which you can think of as an implicit form of channel estimation), and the precoding matrix.
Precoding with graphs
To make the system generalize to different numbers of users, we use a special type of graph neural network (GNN). This network outputs the optimal precoding coefficients for each user and flexibly adapts to a varying number of users without requiring retraining.
While we’re not the first to apply GNNs to precoding, our approach is unique. Earlier studies (Shen et al., 2021; Liu et al., 2024) have shown the benefits of using GNNs, but they often treat precoding as an isolated task. What makes our research different is how we integrate the GNN into the full end-to-end pipeline. Instead of treating precoding as an isolated block, we allow the system to jointly learn pilot optimization and precoding together.
End-to-end system block-by-block
The different blocks of the proposed end-to-end system are illustrated in Figure 1.
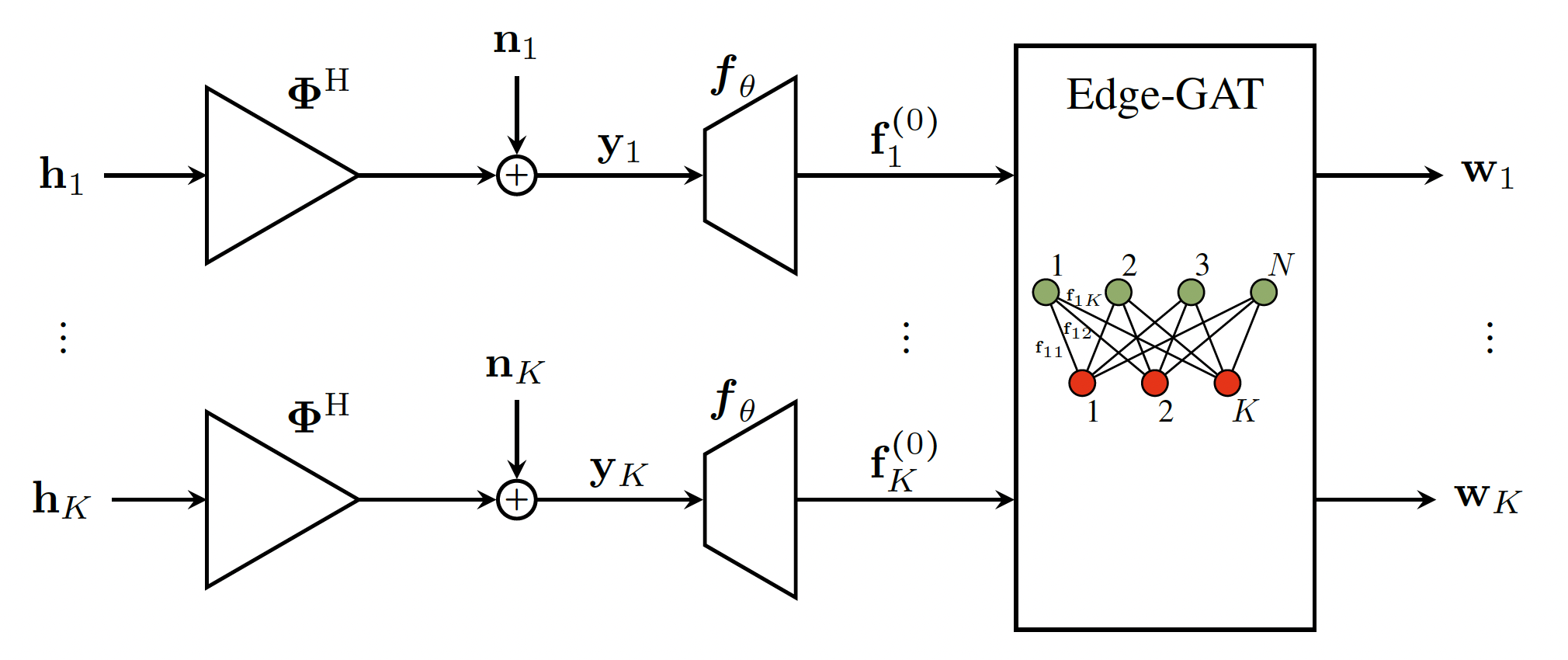Block diagram of the end-to-end model.
1. Pilot training
The first stage is pilot training. At this stage the base station sends out a set of reference signals (called pilots) so that each user can “sense” the channel conditions between itself and the base station.
What the user receives is a mix of two things:
- a transformed version of the CSI, and
- some background noise (inevitable in any wireless system).
The pilots are represented by a learnable matrix $\mathbf{\Phi}$, modeled as a complex fully connected layer without bias.
2. Feedback
Once each user receives its pilot signals, it sends the observation $\vy_k$ back to the base station. For simplicity, we assume this feedback is perfect (i.e., no errors or delays).
3. Feature extraction
Once the base station has received feedback from all users, it passes these observations through a feature extractor $\boldsymbol{f}_{\theta}$, implemented as a small neural network.
This module turns the simple, low-dimensional feedback into a richer set of features, giving the system a more detailed and useful representation of the channel.
The same feature extractor is applied to every user, keeping the system efficient and scalable, even as the number of users grows.
4. Precoding design with Edge-GAT
Next, we model the communication system as a bipartite graph:
- One set of nodes represents the base station antennas.
- The other set represents the users.
- The edges connecting antennas and users carry the features extracted in the previous stage.
To process this graph we use an edge graph attention network (Edge-GAT). Unlike typical GNNs that update node information, the Edge-GAT focuses on updating edges, allowing it to capture the intricate relationships between each antenna and each user.
Through multiple layers, the edge features are refined until they converge on the values that form the precoding matrix $\vW$, which tells the base station how to optimally shape and transmit signals to all users.
Finally, the precoding matrix is normalized (to respect the power constraint), and the overall performance is measured by the sum rate, i.e., the total data rate achieved across all users. Note that, we use the negative of the sum rate as our loss function during training.
Results
The main results of this work are show in Figure 2.
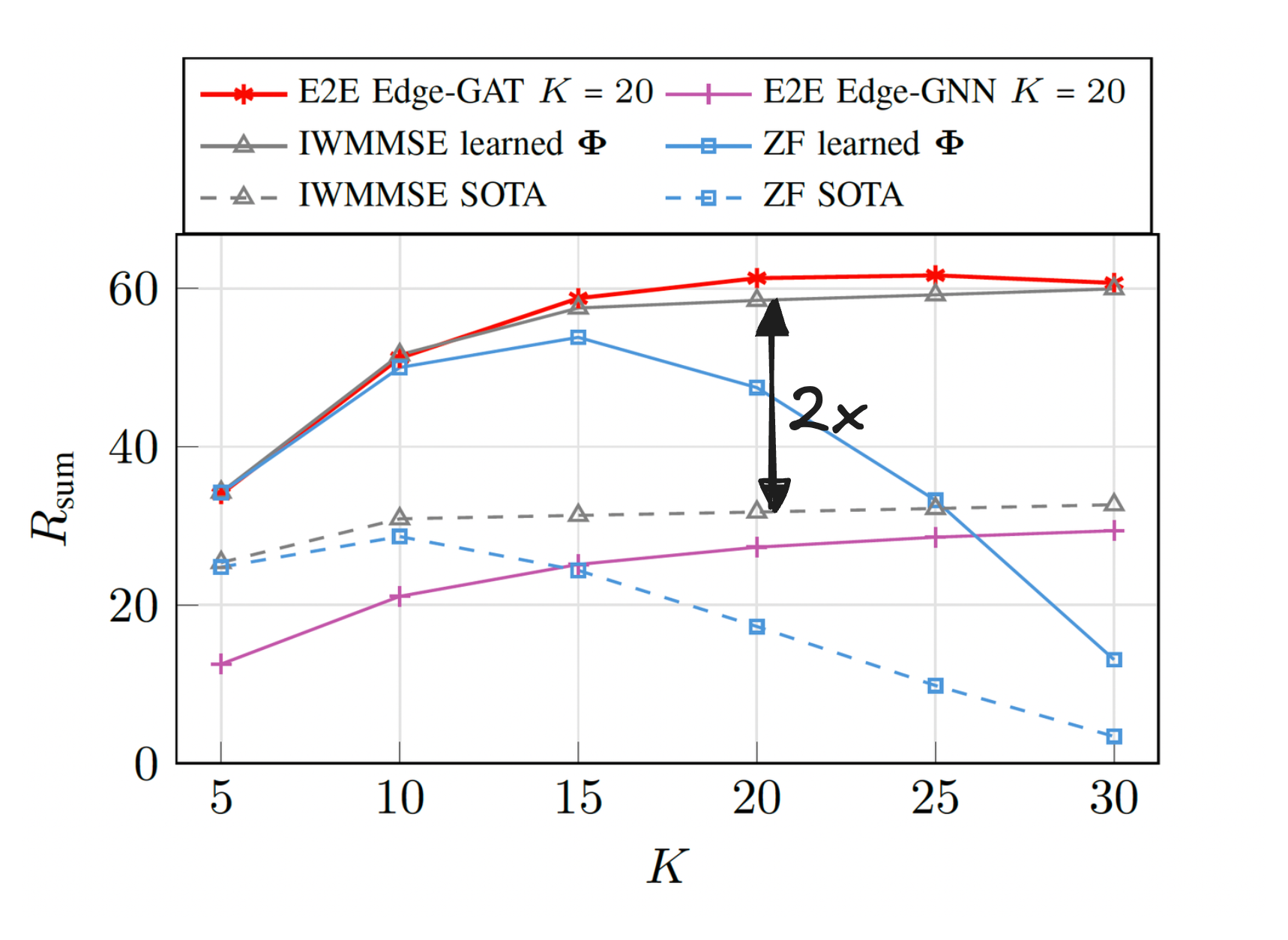Sum rate for different number of users $K$, using 32 pilots. The model was trained with only 20 users.
From these results, we can draw two main conclusions. First, the proposed end-to-end Edge-GAT scales really well with the number of users even though it was only trained in a setting with 20 users.
Second, the precoding based on the learned pilot matrix achieves up to twice the sum rate compared to the one based on DFT pilots.
Why this matters 
We’re really excited about these results for two main reasons:
1) Efficiency
When both our proposed end-to-end model and the traditional Iterative Weighted MMSE (IWMMSE) algorithm use the same learned pilot matrix $\mathbf{\Phi}$, they achieve identical performance. However, the key advantage lies in computational complexity. The traditional IWMMSE is inherently sequential, whereas our method, built on GAT, is fully parallelizable. This parallelism translates to significant speed and efficiency gains when deployed on modern hardware, making it much more practical in real-time systems with many users.
2) The power of learned pilots
Next, we see the advantages of the learned pilot matrix compared to traditional one. This indicates that the usage of the learning-based approach can help to find a more specific solution for the proposed scenario which is an advantage of data-based models.
References
- Rizzello, V., Ben Amor, D., Joham, M., & Utschick, W. (2024). Scalable Multi-User Precoding and Pilot Optimization with Graph Neural Networks. ICC 2024 - IEEE International Conference on Communications, 2956–2961. https://doi.org/10.1109/ICC51166.2024.10622529
- Shen, Y., Shi, Y., Zhang, J., & Letaief, K. B. (2021). Graph Neural Networks for Scalable Radio Resource Management: Architecture Design and Theoretical Analysis. IEEE Journal on Selected Areas in Communications, 39(1), 101–115. https://doi.org/10.1109/JSAC.2020.3036965
- Liu, S., Guo, J., & Yang, C. (2024). Multidimensional Graph Neural Networks for Wireless Communications. IEEE Transactions on Wireless Communications, 23(4), 3057–3073. https://doi.org/10.1109/TWC.2023.3305124
Frequency division duplexing is a communication technique that uses separate frequency bands for simultaneous uplink (from user to base station) and downlink (from base station to user) transmissions. ↩