Gumbel-Softmax Trick

This post explains the Gumbel-Softmax trick, a method to sample from a categorical distribution using a differentiable function of noise. Starting from the Gumbel-Max trick, which samples exactly but is not differentiable, it introduces the Gumbel-Softmax as a continuous, differentiable approximation. This is especially useful in deep learning for enabling gradient-based optimization when working with discrete variables.

The Gumbel-Max trick

Suppose that we want to sample from a categorical distribution with class probabilities $\pi_1, \dots \pi_k$, where $\sum_{i=1}^k \pi_i=1$. Essentially, we want to randomly pick one class according to those probabilities, but we want to do so using a deterministic function of noise (reparameterization), which is useful in deep learning.

If you are already familiar with the variational autoencoder (VAE), you know that it uses the reparameterization trick to sample a point $z\sim \mathcal{N}(\mu, \sigma^2)$. Here, we want to do the same but for $y\sim \text{Categorical}(\boldsymbol{\pi})$.

The Gumbel-Max trick (Maddison et al., 2014) allows to sample from a categorical distribution defined by $\boldsymbol{\pi}$.

• Step 1: Draw i.i.d. samples $g_i \sim \text{Gumbel}(0,1)$, one for each class $i$.
• Step 2: Compute $y = \arg\max_i \log\pi_i + g_i$.

Why it works:

The reason it works is that $\mathbb{P}(i=\arg\max_j z_j) = \pi_i$, where $z_i = \log \pi_i + g_i$ and $g_i \sim \text{Gumbel}(0,1)$.

Proof:

Step 1. Transforming Gumbel variables into a form involving uniform variables

• Apply transformation: $X_i = -\log(-\log U_i)$, where $U_i \sim \text{Uniform}(0,1)$
• Therefore: \(\begin{align} z_i &= \log\pi_i + g_i\\ &= \log\pi_i + X_i\\ &= \log\left(\frac{\pi_i}{-\log U_i}\right) \end{align}\)
• Apply exp on both sides: $\exp(z_i) = \frac{\pi_i}{-\log U_i}$.

Step 2. Rewriting the sampling condition in terms of inequalities

If $i = \arg\max_j z_j$, that means

\[\begin{equation} \frac{\pi_i}{-\log U_i} > \frac{\pi_j}{-\log U_j} \quad \forall j \ne i. \end{equation}\]

Rewriting: \(\begin{equation} \frac{-\log U_j}{\pi_j} > \frac{-\log U_i}{\pi_i} \quad \forall j \ne i. \end{equation}\)

Now define: \(\begin{equation} T_i = \frac{-\log U_i}{\pi_i}, \end{equation}\)

so the condition becomes: \(\begin{equation} T_i < T_j \quad \forall j \ne i. \end{equation}\)

Step 3. Characterizing the distribution of $T_i$

​Since $U_j$ are uniform, the transformed variables $T_j$ turn out to be exponentially distributed with rate $\pi_j$. Therefore, we have that \(\begin{equation} f_{T_i}(t) = \pi_i e^{-\pi_i t}. \end{equation}\)

Step 4. Computing the probability that $T_i$ is the minimum

Now we want to show that $\mathbb{P}(i=\arg\min_j T_j) = \pi_i$.

Instead of thinking about all random variables at once, we condition on one of them (say, $T_i$) having a specific value, and then compute the chance that all the other ones are greater than that value. We then average (integrate) this over all possible values of $T_i$.

By assuming $T_i = t$ we have that:

\[\begin{equation} P(T_j > t \ \forall j \ne i \mid T_i = t) = \prod_{j \ne i} P(T_j > t) = \prod_{j \ne i} e^{-\pi_j t} = e^{-t \sum_{j \ne i} \pi_j}. \end{equation}\]

So we compute the total probability by integrating: \(\begin{equation} P(T_i = \min_j T_j) = \int_0^\infty \underbrace{P(T_j > t \ \forall j \ne i \mid T_i = t)}_{\text{others bigger than } t} \cdot \underbrace{f_{T_i}(t)}_{\text{probability that } T_i = t} \, dt. \end{equation}\)

This is exactly: \(\begin{equation} P(T_i = \min_j T_j) = \int_0^\infty \left( e^{-t \sum_{j \ne i} \pi_j} \right) \cdot \left( \pi_i e^{-\pi_i t} \right) dt \end{equation}\)

which becomes: \(\begin{equation} = \pi_i \int_0^\infty e^{-t \sum_j \pi_j} \, dt = \pi_i \cdot \frac{1}{\sum_j \pi_j}. \end{equation}\)

This concludes the proof.

Problem:

The Gumbel-Max trick provides discrete samples, which are not differentiable (bad for backpropagation).

The Gumbel-Softmax Trick

The Gumbel-Softmax (Jang et al., 2017) provides a differentiable approximation to the Gumbel-Max trick.

Instead of taking the argmax, we take the softmax:

\(\begin{equation} y_i = \frac{\exp((\log \pi_i + g_i)/\tau)}{\sum_{j=1}^k\exp((\log \pi_j + g_j)/\tau)}, \end{equation}\) where $g_i \sim \text{Gumbel}(0,1)$, and $\tau$ is a temperature parameter, and $\boldsymbol{y} \in \mathbb{R}^k$ is a differentiable vector that approximates a one-hot sample from the categorical distribution.

Observations:

• As $\tau \rightarrow 0$ the distribution becomes one-hot, approaching Gumbel-Max (hard sampling).
• As $\tau \rightarrow \infty$ the distribution becomes uniform.

The next picture shows how the temperature parameter influences the output $\boldsymbol{y}$.

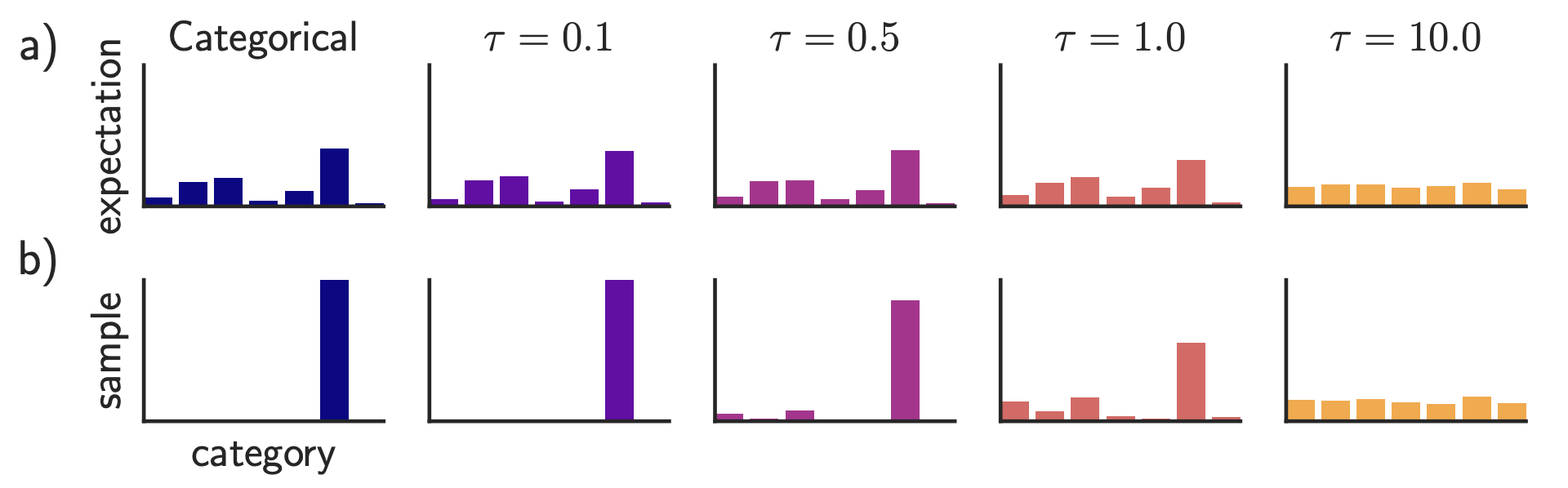Extracted from (Jang et al., 2017)

In the Figure, row a) shows the expectation (average value over many samples) from the Gumbel-Softmax, whereas row b) shows a single sample from the Gumbel-Softmax.

Each column corresponds to a different temperature $\tau$, and the leftmost column is the true categorical distribution (used as reference).

Interpretation of Each Column:

Leftmost:

• a) Expectation shows the true class probabilities (bars with varying heights).
• b) The sample is a one-hot vector (only one category is 1, others are 0).

Low temperature ($\tau=0.1$, $\tau=0.5$):

• a) The Gumbel-Softmax expectation is close to the original categorical probabilities. This means it mimics the categorical distribution well.
• b) The samples are almost one-hot, with one bar near 1 and others near 0.

Moderate temperature ($\tau=1.0$):

• a) The expectation is still biased toward the original categorical probabilities but more smoothed.
• b) The sample is soft (not one-hot): the max bar is less than 1, others are slightly above 0.

High temperature ($\tau=10$):

• a) The expectation becomes uniform.
• b) The sample is also flat across categories.

References

1. Maddison, C. J., Tarlow, D., & Minka, T. (2014). A∗Sampling. Advances in Neural Information Processing Systems, 27.
2. Jang, E., Gu, S., & Poole, B. (2017). Categorical Reparameterization with Gumbel-Softmax. 5th International Conference on Learning Representations, ICLR 2017, Toulon, France, April 24-26, 2017, Conference Track Proceedings.