Geometric Distribution and Nested Dropout

This post derives the CCDF of the geometric distribution, including its truncated form for finite support. It also provides some insights regarding the usage of the geometric distribution in the Nested Dropout layer, which has been introduced to prioritize lower-index features in neural networks.

The geometric distribution gives the probability that the first occurrence of success requires ${\displaystyle k}$ independent trials, each with success probability ${\displaystyle p}$. The probability mass function (pmf) is

$$\begin{equation} \label{eq:geo} \Pr(X=k)=(1-p)^{k-1}p \end{equation}$$

for ${\displaystyle k=1,2,3,4,\dots }$

The CDF is

$$\begin{equation} \label{eq:geo-cdf} \Pr(X\leq k)=\sum_{j=1}^k(1-p)^{j-1}p. \end{equation}$$

Hence, the CCDF is

$$\begin{equation} \label{eq:geo-ccdf} \Pr(X > k)= 1 - \sum_{j=1}^k(1-p)^{j-1}p = \sum_{j=k+1}^{\infty}(1-p)^{j-1}p = (1-p)^k. \end{equation}$$

Proof:

\[\begin{align*} S &= \sum_{j=k+1}^{\infty}(1-p)^{j-1}p\\ &= p\sum_{j=k+1}^{\infty}(1-p)^{k + j - (k + 1)} \quad \text{add and subtract } k\\ &= p(1-p)^k \sum_{j=0}^{\infty}(1-p)^j\\ &= p(1-p)^k \frac{1}{1 - (1 - p)} \quad \quad \text{use formula for infinite geometric series}\\ &= (1-p)^k. \end{align*}\]

Since $\Pr(X > k) = (1-p)^k$, then $\Pr(X \ge k) = (1-p)^{k-1}$.

Derivation for finite support

Now let’s assume that the geometric distribution is truncated to the finite set ${1,2, \dots ,K}$.

In this case the pmf must be normalized, so the sum over the finite support is 1:

$$\begin{equation} \label{eq:geo2} \Pr(X=k)= \frac{(1-p)^{k-1}p}{\sum_{j=1}^K p(1-p)^{j-1}} = \frac{(1-p)^{k-1}p}{1 - \sum_{j=K+1}^{\infty} p(1-p)^{j-1}} = \frac{(1-p)^{k-1}p}{1 - (1 - p)^K}. \end{equation}$$

Therefore, we obtain:

$$\begin{equation} \label{eq:geo-ccdf2} \Pr(X \ge k) = \frac{\sum_{j=k}^K(1-p)^{j-1}p}{1 - (1 - p)^K}. \end{equation}$$

We can rewrite the numerator as:

\[\begin{align*} N &= \sum_{j=k}^K(1-p)^{j-1}p\\ &= p \sum_{j=k}^K(1-p)^{j - k + k-1}\\ &= p (1-p)^{k-1}\sum_{j=k}^K(1-p)^{j -k}\\ &= p (1-p)^{k-1}\sum_{j=0}^{K-k}(1-p)^{j} \quad \text{change index to simplify sum}\\ &= p (1-p)^{k-1} \frac{1 - (1-p)^{K - k + 1}}{1 - (1-p)} \quad \text{using } \star\\ &= p (1-p)^{k-1} \frac{1 - (1-p)^{K - k + 1}}{p}\\ &= (1-p)^{k-1} (1 - (1-p)^{K - k + 1}), \end{align*}\]

where $\star$ denotes the geometric formula: $\sum_{j=0}^n r^j = \frac{1 - r^{n+1}}{1-r}$.

By plugging this result back into \eqref{eq:geo-ccdf2} we obtain:

$$\begin{equation} \label{eq:geo-ccdf2-fin} \Pr(X \ge k) = (1-p)^{k-1} \frac{1 - (1-p)^{K - k + 1}}{1 - (1 - p)^K}. \end{equation}$$

Nested Dropout Insights

Nested Dropout, introduced in (Rippel et al., 2014), is a structured alternative to standard dropout. Rather than randomly dropping individual units, it drops entire trailing segments of a vector, enforcing an explicit ordering of features.

A cutoff index $k$, typically sampled from a geometric distribution, determines how many of the first units to keep—zeroing out the rest. This creates a nested hierarchy where lower-indexed features are more likely to survive, pushing the model to encode the most essential information early in the vector.

In this example we assume that our input consists of 128 neurons, and we see how the choice of the distribution parameters influences the CCDF. In particular, we experiment with Geo(p=0.01), Geo(p=0.02), and Uniform distributions. The figure below shows the results of the CCDF using formula \eqref{eq:geo-ccdf2-fin}.

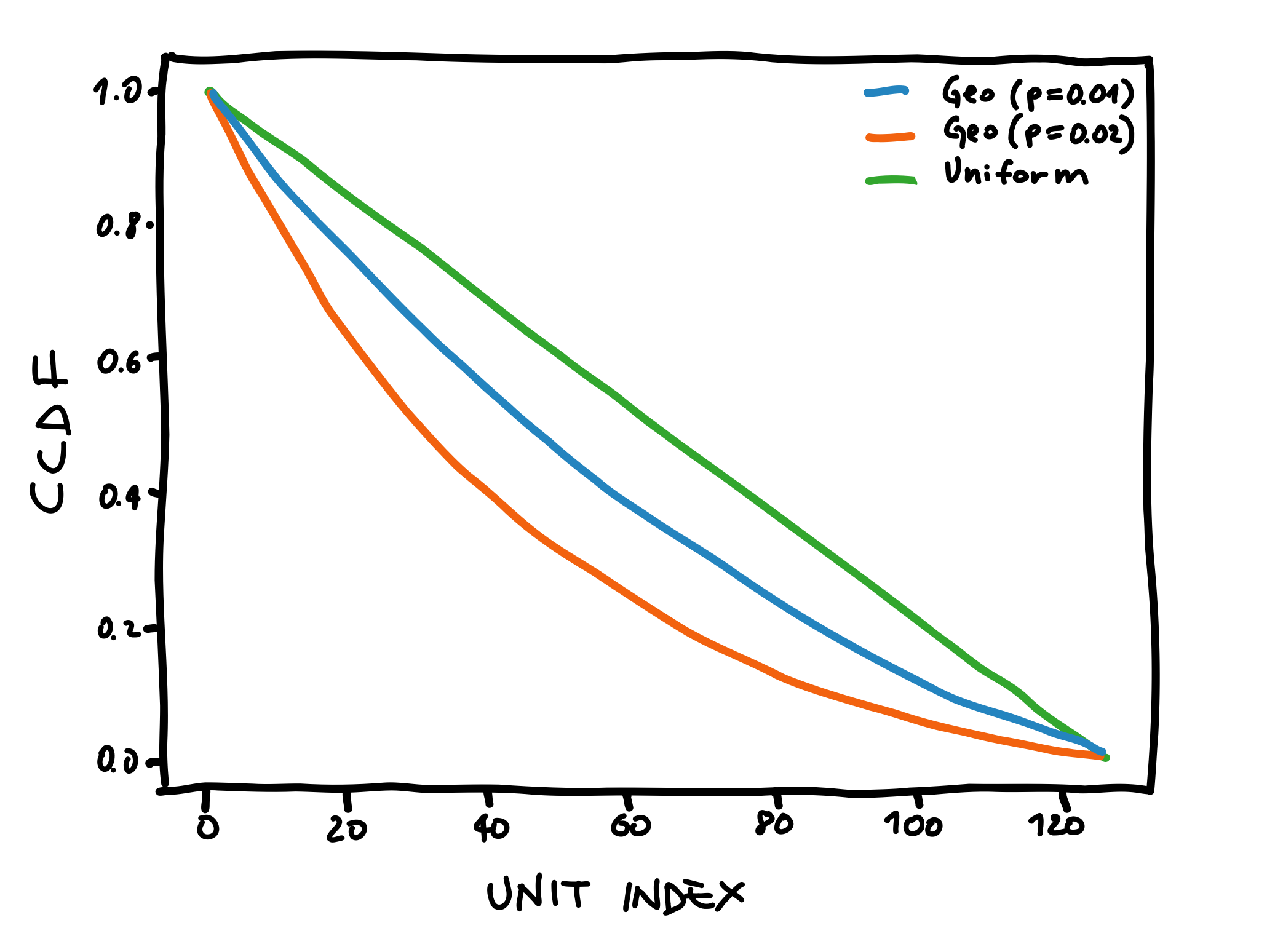CCDF for different distributions.

What we can observe is that the geometric distribution assigns exponentially decreasing probabilities to higher-index dimensions.

References

1. Rippel, O., Gelbart, M., & Adams, R. (2014). Learning Ordered Representations with Nested Dropout. 31st International Conference on Machine Learning, ICML 2014, 5.